1Les eaux souterraines représentent le deuxième réservoir d'eau douce sur Terre après celui des glaciers polaires. Les aquifères sont donc exploités pour l'irrigation mais surtout pour l'alimentation en eau potable des populations. Cette ressource, indispensable à la vie, est trop souvent sujette à des problématiques de pollutions domestiques, industrielles ou agricoles. La préservation de cette ressource nécessite de bien comprendre les processus de transfert de polluants.
2Tous les réservoirs souterrains ne sont pas des aquifères. Tout d'abord, le terme aquifère signifie que le fluide contenu dans la roche est de l'eau. En effet, le fluide n'est pas forcément de l'eau, il peut également être gazeux ou pétrolifère. Ensuite, un aquifère indique que la roche est poreuse et perméable, c'est-à-dire qu'elle peut contenir une quantité importante d'eau (porosité) et que cette eau est mobilisable (perméabilité). Ces deux propriétés importantes qui caractérisent un aquifère sont inhérentes à la structure géométrique interne de la roche : on parle de milieux poreux et/ou de milieux fracturés. Cette géométrie est primordiale car c'est elle qui va guider la dynamique du fluide : on comprend bien qu'il est plus facile de décrire cette dynamique dans un tuyau parfaitement cylindrique que dans un milieu dont on ne connait pas la forme.
3Certains modèles de transfert de masse dans les milieux poreux et/ou fracturés prennent en compte cette géométrie complexe pour simuler les écoulements. On peut citer par exemple les modèles géométriques fractals qui ont été largement utilisés dans cette thématique (e.g. Fleurant and Jeong, 2001 ; Jin et al., 2015 ; Cihan et al., 2009 ; Hsu and Chen, 2010 ; Hunt and Gee, 2002). Toutefois, devant la grande difficulté à représenter la structure poreuse ou à la modéliser, la plupart des modèles de transfert de fluide en milieux poreux est basée sur l'équation classique de convection-dispersion. Cette équation prend en compte le comportement du fluide dans le milieu plutôt que le milieu lui-même. Ainsi, plutôt que de modéliser la forme du milieu poreux, on simule l'hydrodynamique qui découlerait de la complexité de ce milieu. Ces modèles de transfert en milieu poreux utilisent trois processus de déplacement : la convection, la diffusion moléculaire et la dispersion (Goblet, 1981).
4Dans les aquifères, les fluides sont en mouvement. Même s’il est extrêmement lent, ce déplacement est dû au gradient de la charge hydraulique ; on parle alors de convection. La convection est l’entraînement d’une masse par le seul mouvement du fluide (éq. 12). La diffusion moléculaire est un phénomène physique lié à l’agitation thermique moléculaire. Dans un liquide au repos, les particules de fluide subissent un mouvement brownien et sont déplacées uniformément dans toutes les directions de l’espace. Le résultat de cette agitation moléculaire est le transfert de particules des zones de fortes concentrations vers les zones de plus faibles concentrations. Dans un milieu poreux saturé en eau, cette agitation moléculaire ne peut se faire de façon isotrope à cause des grains solides du milieu. Pour tenir compte de ce phénomène qui réduit la possibilité qu’a une particule à diffuser, on définit un coefficient de diffusion moléculaire effectif caractérisant la diffusion de l’élément dans le milieu considéré (éq. 13). Lorsqu’un fluide est en mouvement, différents mélanges viennent s’ajouter au processus purement diffusif que nous venons de décrire, on parle alors de dispersion cinématique. La dispersion cinématique est la conséquence de la non-uniformité du champ des vitesses dans le milieu poreux à différentes échelles :
-
L’espace entre deux grains de milieu poreux peut être considéré comme un capillaire. La vitesse est nulle à la surface et augmente vers le centre où elle est maximale ;
-
La géométrie des grains produit des variations de direction et de module des vitesses locales.
5Lorsque la dispersion cinématique opère dans la direction principale de l’écoulement, on parle de dispersion longitudinale. Dans le cas d’une dispersion cinématique dans le plan normal à la direction principale d’écoulement, on parle de dispersion transversale. Si l’on veut considérer l’écoulement d’un soluté en milieu poreux saturé, on ne peut pas séparer la diffusion moléculaire de la dispersion cinématique. On regroupe donc ces deux phénomènes sous le terme de dispersion hydrodynamique (éq. 14).
6Si on prend en compte les trois processus que l’on vient de développer (convection, diffusion et dispersion), on peut écrire mathématiquement le déplacement d’un fluide en milieu poreux saturé (éq. 19) :
7L’équation de transfert peut être résolue numériquement par différentes méthodes : différences finies, éléments finis ou marche au hasard. Lorsque le problème posé est assez simple (paramètres constants dans l’espace et le temps, conditions initiales et aux limites simples), il existe des solutions exactes de l’équation de transfert, appelées solutions analytiques. Elles permettent de déterminer la valeur de la concentration en un point de l’espace, à un temps donné. Les solutions analytiques existent pour des cas mono-, bi- et tridimensionnels et pour des injections ponctuelles instantanées et ponctuelles à durée variable (Annexe 1).
8L'objectif de cet article est de présenter un modèle de transfert de polluant en milieu poreux, en utilisant une approche multi-agents. L'article est structuré suivant le formalisme ODD (Grimm et al., 2006). Le modèle représente une situation simple d'un aquifère dont les eaux souterraines sont connectées hydrauliquement à un cours d'eau. Une source de pollution, dont on peut déterminer la taille, est positionnée sur le versant de cet aquifère. Le modèle simule le transfert du nuage de polluant pour différentes propriétés préalablement données (caractéristique de l'aquifère, introduction d'un forage, nature du polluant, etc.) et indique l'évolution de sa concentration en fonction du temps lorsqu'il atteint le cours d'eau. Cette situation simple permet d'illustrer de façon visuelle des scénarios de transfert relativement complexes, le modèle est donc un bon outil pédagogique pour aborder les problématiques de pollutions souterraines auprès des étudiant-e-s. Il est également un bon outil de recherche pour donner des ordres de grandeurs et étudier des comportements hydrodynamiques simples.
9L'objectif principal du modèle est de prédire l'évolution spatio-temporelle d'une source de polluant dans un aquifère (Figure 1). Le modèle proposé permet de simuler les processus de transfert, c'est-à-dire la convection, la diffusion et la dispersion. Ces processus sont modélisés dans le cadre simplifié d'un aquifère homogène (même composition en tout point de l'espace) et isotrope (invariance des propriétés en fonction de la direction). Le contexte de la simulation se fait pour une condition aux limites de Dirichlet : une rivière impose un potentiel constant, c'est-à-dire que le niveau de la rivière reste à une hauteur constante. Enfin, un forage (terme source) est introduit dans cet aquifère comme élément d'exploitation de l'eau souterraine.
10Le modèle est constitué de deux entités : l'aquifère, qui est le support spatial fixe et dont les propriétés sont constantes dans le temps, et les particules de polluant qui utilisent les propriétés de l'aquifère pour se mouvoir.
11L'aquifère est caractérisé par sa charge hydraulique, c'est-à-dire la hauteur de l'eau (zone saturée) qu'il contient en chaque point. La valeur de la charge hydraulique permet de calculer la vitesse d'écoulement de l'eau souterraine (convection) ainsi que la dispersion qui est produite par cet écoulement dans un milieu poreux (diffusion + dispersion). Ces variables spatiales sont données dans le Tableau 1, et sont déterminées à partir des paramètres de l'aquifère (Tableaux 2 et 3).
Figure 1 : Caractéristiques du système modélisé. Un aquifère d'épaisseur moyenne e que l'on étudie sur une extension de 400 m par 400 m. Dans un aquifère, les eaux souterraines s'écoulent des charges hydrauliques les plus fortes vers les plus faibles, donc vers la rivière qui a ici une charge hydraulique imposée (condition aux limites de Dirichlet) de h = 0 m. Dans le cas présenté ici on voit que sur distance de X = 400 m, la charge hydraulique varie de 3 m, la pente moyenne de l'aquifère est donc de β = 0.0075.

Tableau 1 : Variables spatiales de l'aquifère
|
Nom
|
Nom dans le code Netlogo
|
Unité (S.I.)
|
Symbole mathématique
|
|
Charge hydraulique
|
ChargeHydrau
|
m
|
h
|
|
Vitesse longitudinale (Y)
|
VitesseY
|
m/s
|
VL
|
|
Vitesse transversale (X)
|
VitesseX
|
m/s
|
VT
|
|
Vitesse moyenne
|
VitesseMoy
|
m/s
|
Vm
|
|
Dispersion longitudinale (Y)
|
DispersionLong
|
m2/s
|
DL
|
|
Dispersion transversale (X)
|
DispersionTrans
|
m2/s
|
DT
|
Tableau 2 : Paramètres du système étudié. Les propriétés de l'aquifère données (porosité, perméabilité) correspondent à des valeurs représentatives d'un réservoir calcaire fracturé.
|
Nom
|
Nom dans le code Netlogo
|
Unité (S.I.)
|
Valeur typique
|
Symbole mathématique
|
|
Dimension X
|
|
m
|
400
|
x
|
|
Dimension Y
|
|
m
|
400
|
y
|
|
Epaisseur (Z)
|
EpaisseurAquifere
|
m
|
50
|
e
|
|
Perméabilité
|
Permeabilite
|
m/s
|
10-4
|
k
|
|
Transmissivité
|
Transmissivite
|
m2/s
|
5.10-3
|
T
|
|
Dispersivité
|
Dispersivite
|
m
|
1.0
|
α
|
|
Porosité
|
Porosite
|
-
|
0.15
|
ω
|
|
Pente
|
Pente
|
-
|
10-2
|
β
|
|
Localisation X
|
PositionForageX
|
m
|
0
|
xf
|
|
Localisation Y
|
PositionForageY
|
m
|
250
|
yf
|
|
Débit du forage
|
DebitForage
|
m3/s
|
2.10-3
|
q
|
Tableau 3 : Paramètres du polluant
|
Nom
|
Nom dans le code Netlogo
|
Unité (S.I.)
|
Valeur typique
|
Symbole mathématique
|
|
Localisation X
|
PositionSourceX
|
m
|
300
|
xs
|
|
Localisation Y
|
PositionSourceY
|
m
|
300
|
ys
|
|
Facteur de retard
|
FacteurRetard
|
-
|
1.0
|
R
|
|
Nombre de particules
|
NombreParticules
|
-
|
2 000
|
N
|
|
Taille de la source
|
TailleSource
|
m
|
30
|
|
|
Trace de la trajectoire
|
Trace
|
-
|
FALSE
|
|
12Les étapes du modèle sont décrites sur le logigramme de la Figure 2. Ces étapes permettent l'établissement d'une succession de processus :
-
Le système aquifère – source de polluant est préalablement caractérisé par l'utilisateur grâce à des paramètres. Ces paramètres permettent une configuration spatiale du système mais aussi le réglage des propriétés du système ;
-
Les valeurs des paramètres conduisent aux valeurs de la charge hydraulique, et consécutivement à celles des vitesses et des coefficients de dispersion. Chacune de ces variables est spatialisée et est donc affectée à chacun des patches (patches-own). En effet, la charge hydraulique, les vitesses et les coefficients de dispersion ont des valeurs qui dépendent de leur position par rapport à la rivière et au forage.
-
Les agents mobiles (particules) utilisent pour se mouvoir les propriétés de convection (vitesses) et de diffusion-dispersion (coefficients de dispersion) du patch sur lequel ils se trouvent. Ce transfert est réalisé à pas de temps discrets (ticks), convertis ensuite en temps continu : temps = ticks * PasTempsJ. Pour des raisons d'homogénéité des calculs, les unités des variables et des paramètres sont toutes données en Unité du Système International (U.S.I.).
Figure 2 : Logigramme du modèle

13L'émergence : les propriétés de déplacement des agents mobiles (particules) sont individuelles et dépendantes de leur position locale (patch). Le nuage de polluant est donc discrétisé en particules qui transportent une proportion de la masse du polluant. Si par exemple la source du polluant est de 100 kg et qu'on modélise le nuage du polluant par 1 000 particules, on estime alors que chaque particule transporte une quantité équivalente de 100 / 1 000 = 0.1 kg, soit 100 g. La structure du nuage de polluant ou de particules est dépendante des vitesses de l'eau souterraine dans l'aquifère et des coefficients de dispersion, eux-mêmes dépendants des nombreux autres paramètres spatiaux et physico-chimiques. Le champ des vitesses et les coefficients de dispersion font donc émerger la forme globale du nuage de polluant qui dépend des conditions locales sur les patches. La distribution spatio-temporelle des concentrations du nuage de polluant (variable globale) est donc issue des multiples configurations possibles des particules et de leurs variables locales.
14Adaptation : les agents mobiles (particules) adaptent leur condition de déplacement aux propriétés locales qu'ils tirent des patches sur lesquels ils se trouvent. Ces propriétés sont caractérisées par leurs vitesses longitudinale et transversale ainsi que par leurs coefficients de dispersion longitudinale et transversale.
15Perception : les agents statiques (patches) localisés sur la rivière et aux alentours du forage ont une action de perception des agents mobiles (particules). Lorsque ces derniers sont dans un rayon égal à la valeur de RayonPuits mètres du forage, ils sont détruits (die) puisqu'ils sortent du système aquifère. Lorsque les agents mobiles arrivent dans la rivière ils sont également détruits pour les mêmes raisons que précédemment mais avant cela, ils sont comptabilisés afin de déterminer la concentration du polluant dans la rivière.
16Interaction : Il n'y a pas d'interaction des agents mobiles (particules) entre eux. En revanche l'interaction entre le polluant (agents mobiles particules) et le milieu poreux (agents statiques patches) est modélisée par le biais d'un coefficient de retard R. Le transfert d'un polluant n'est pas conservatif (il se dégrade) et il est réactif (il a des échanges avec la matrice solide du milieu poreux). Dans les modèles géochimiques, on associe donc au transfert soit des phénomènes d'interactions simples (coefficient de retard, isothermes de Langmuir ou de Freundlich), ou plus complexes comme la spéciation. La réaction d’un soluté avec le milieu regroupe un ensemble de processus physico-chimiques qui retiennent le soluté sur les grains solides du milieu poreux. Parmi ces réactions on peut citer les échanges cationiques (les ions positivement chargés qui viennent en contact avec des surfaces négatives, des argiles par exemple) et les réactions chimiques (précipitation, dissolution, oxydoréduction). Dans le cas le plus simple et le plus fréquent, ces réactions sont considérées comme instantanées et réversibles. Cela signifie que les cinétiques de réactions sont très rapides et de même ordre de grandeur entre soluté et solide. Il apparaît dans ce cas un retard du soluté par rapport à un traceur non réactif. Ce retard s’exprime dans l’équation de transfert par un facteur appelé coefficient de retard R. Ce coefficient divise les vitesses et donc les coefficients de dispersion et agit ainsi comme une résistance au déplacement dans le milieu poreux. On note que le cas où R = 1, correspond à un polluant qui a les mêmes conditions hydrodynamiques et hydrodispersives que l'eau souterraine.
17Stochasticité : le principe même du présent modèle de transfert des particules est basé sur une approche stochastique puisque leur déplacement se fait par une marche aléatoire lagrangienne. Le transfert des particules de polluant se fait suivant deux processus : la convection et la diffusion-dispersion. La partie convective est la partie déterministe du processus, elle ne dépend que de la valeur des vitesses, constantes sur un patch donné. La partie diffuso-dispersive est destinée à modéliser la complexité du milieu poreux dans lequel les particules se déplacent. La diffusion des particules tend à homogénéiser leur concentration dans l'espace (Figure 3 : Lors de la diffusion moléculaire, les particules tendent à occuper tout l'espace et donc à homogénéiser la concentration.). La diffusion est modélisée par un mouvement brownien et grâce à une marche aléatoire. Le processus de dispersion des particules se fait à deux échelles différentes (Figure 4). Au sein du pore, l'espace interstitiel a un comportement identique à celui d'un tube. On y retrouve donc un profil des vitesses de type Poiseuille, c'est-à-dire des vitesses plus rapides au milieu du pore et plus faibles à mesure qu'on se rapproche du grain solide du milieu poreux. A l'échelle d'un volume élémentaire représentatif de milieu poreux, et bien que le nuage de particules se déplace à une vitesse constante (en direction et en module), les particules empruntent elles des trajectoires très différentes du fait de la tortuosité du milieu poreux.
Figure 3 : Lors de la diffusion moléculaire, les particules tendent à occuper tout l'espace et donc à homogénéiser la concentration.

Figure 4 : La dispersion des particules se fait à deux échelles différentes. Au sein du pore (à gauche), et du fait de la tortuosité des chemins à parcourir (à droite).

Collectivité : le nuage de polluant est composé de particules individuelles qui, par leur comportement local, engendrent une forme particulière du nuage à une échelle macroscopique. Le passage des variables locales aux variables globales se fait par un simple calcul de moyenne. En effet, si le nuage est composé de n particules i de coordonnées (xi,yi), on peut en déduire par exemple le centre de gravité du nuage de particules qui sera de coordonnées ( ). Les variables locales ou microscopiques sont (xi,yi) et les variables globales ou macroscopiques sont (X, Y).
). Les variables locales ou microscopiques sont (xi,yi) et les variables globales ou macroscopiques sont (X, Y).
18Chaque simulation débute par une initialisation des variables (conditions initiales et conditions aux limites) qui va contrôler le comportement de la simulation. Cette phase d'initialisation se fait par le biais des fonctions InitialisationVariables et InitialisationPatches. Elle consiste à calculer la charge hydraulique et les vitesses pour chaque patch, en fonction des paramètres qui ont été entrés par l'opérateur.
19Il n'y a pas d'entrées à proprement dit dans ce modèle, c'est-à-dire de données extérieures qui viendraient modifier dans le temps ou dans l'espace les conditions d'une simulation.
20Ce transfert est modélisé par l’équation dite de convection-dispersion ou équation de transfert (éq. 1):
|
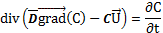
|
éq. 1
|
21Dans une vision très dichotomique, on peut dire qu'il existe deux types d’approches de résolution numérique de l’équation de transfert :
-
Les méthodes aux différences finies et aux éléments finis. Elles ont l’inconvénient d’être peu précises pour les grands nombres de Péclet (cas où la convection domine sur la dispersion). En effet, leurs résultats sont biaisés par la dispersion numérique lorsque la convection devient prédominante. Cette dispersion numérique est liée à la double nature de l’équation de transfert : la dispersion donne une équation hyperbolique et la convection donne une équation parabolique. Ce problème ne peut être résolu que par un affinement poussé du maillage et donc avec de lourds temps de calculs.
-
Les méthodes explicites ou encore appelées individu-centré, marcheur aléatoire, à base d'agents.
22Les méthodes à base d'agents ou de marche au hasard ("particle tracking", "random walk") sont issues de la physique statistique. Le polluant est représenté par des particules, des individus, des agents qui ont un mouvement de convection auquel s’ajoutent des fluctuations aléatoires rendant compte de la dispersion des vitesses dans le milieu poreux et de la diffusion moléculaire (Ackerer & Kinzelbach, 1985 ; Kinzelbach, 1986 ; Kinzelbach, 1988 ; Delay, et al., 1994). Les propriétés statistiques du déplacement global du nuage de polluant sont connues et régies par les propriétés du milieu et les paramètres d’écoulement. Ces méthodes ne sont pas sujettes à la dispersion numérique dont souffrent les méthodes des différences finies ou aux éléments finis, mais elles génèrent des fluctuations de concentrations dues aux déplacements aléatoires des particules, fluctuations qui peuvent être atténuées en augmentant le nombre de particules. Ces oscillations sont générées dans les zones de basses concentrations (faible densité de particules). La méthode de marche au hasard demande, en général, un temps de calcul plus long qu’avec les autres méthodes. Mais la puissance de calcul croissante des ordinateurs donne à cette méthode une actualité scientifique riche et un avenir prometteur (Rahmatian, et al., 2015 ; Bodin, 2015).
23La méthode de marche au hasard est une méthode issue de la physique statistique utilisée pour les phénomènes de diffusion et de dispersion. La description déterministe du transfert d’un polluant en milieu poreux est rendue impossible du fait de la complexité de la géométrie du milieu. Puisque le mouvement d’un polluant ne peut pas être déterministe, la meilleure approche est de considérer la probabilité des mouvements possibles dans le milieu poreux. La méthode de marche au hasard traite l’équation de transfert de façon hyperbolique. Elle consiste à remplacer le nuage de polluant par un nombre de particules discrètes qui subissent un déplacement par convection, avec une vitesse moyenne, auquel s’ajoutent des fluctuations aléatoires (diffusion et dispersion) autour de ce mouvement moyen (Ackerer, et al., 1990).
24On considère X(t), une variable aléatoire qui représente la position de la particule au temps t. Soit ti, i = 0,…, N l’ensemble des dates successives, chacune d’entre elles correspondant à un déplacement S(ti) de la particule : on parle de saut. Si les intervalles de temps sont égaux, alors Δt = (ti-1 - ti). On peut déterminer la trajectoire complète de la particule par :

25Les déplacements de la particule sont supposés indépendants les uns des autres, on parle de processus markovien (Zhang, 2005) et dans ce cas la densité de probabilité s’écrit alors

26L’écriture explicite dans un espace-temps discrétisé est alors :

27Pour le passage en bidimensionnel, l’équation générale s’écrit (Wustmann, 1993) :

La solution explicite à cette équation est donc, en considérant que la dispersion n'est pas fonction de l'espace (les dérivées  sont donc nulles) :
sont donc nulles) :
|

|
(éq. 2)
|
Avec, X(t) et Y(t) les coordonnées cartésienne d'une particule, VL et VT les vitesses longitudinale et transversale respectivement, la vitesse moyenne, Δt le pas de temps,
la vitesse moyenne, Δt le pas de temps,  et
et  les coefficients de dispersion longitudinale et transversale respectivement,
les coefficients de dispersion longitudinale et transversale respectivement, 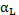 et
et  les dispersivités longitudinale et transversale respectivement, Z1 et Z2 sont des nombres aléatoires de distribution uniforme entre -1 et 1.
les dispersivités longitudinale et transversale respectivement, Z1 et Z2 sont des nombres aléatoires de distribution uniforme entre -1 et 1.
28L’équation de transfert décrit le transport d’un élément conservatif (il ne se dégrade pas) et non réactif (il n’a pas d’échanges avec le solide), ce qui est très rare en réalité. On associe donc au transfert des phénomènes d’interactions simples (coefficient de retard, isothermes de Langmuir et de Freundlich), ou plus complexes comme la spéciation.
29La réaction d’un soluté avec le milieu regroupe un ensemble de processus physico-chimiques qui retiennent le soluté sur les grains solides du milieu poreux. Parmi ces réactions on peut citer les échanges cationiques (les ions positivement chargés qui viennent en contact avec des surfaces négatives, des argiles par exemple) et les réactions chimiques (précipitation, dissolution, oxydoréduction). Dans le cas le plus simple et le plus fréquent, ces réactions sont considérées comme instantanées et réversibles. Cela signifie que les cinétiques de réactions sont très rapides et de même ordre de grandeur entre soluté et solide. Il apparaît dans ce cas un retard du soluté par rapport à un traceur non réactif. Ce retard s’exprime dans l’équation de transfert par un facteur justement appelé coefficient de retard. L’équation devient alors :

Où C est la concentration [ML-3], t le temps [T],  la vitesse moyenne de pore [LT-1], D le tenseur de dispersion [L2T-1] et R le coefficient de retard.
la vitesse moyenne de pore [LT-1], D le tenseur de dispersion [L2T-1] et R le coefficient de retard.
30On voit que le facteur de retard diminue la vitesse moyenne Vm et la dispersion D du soluté (en les divisant). Physiquement, le facteur de retard s’exprime en fonction d’un coefficient de partition qui détermine le partage des quantités entre phase liquide (le soluté) et phase solide (les grains du milieu poreux).
31Le modèle de transfert décrit par l'équation (éq. 2) décrit le déplacement par convection, diffusion et dispersion des particules qui composent le nuage de polluant. Pour les paramètres donnés de la simulation, il convient maintenant de déterminer les variables du transfert : les vitesses d'écoulement.
32Ces vitesses sont calculées grâce à la loi de Darcy. Henri Darcy, en étudiant les fontaines de la ville de Dijon, montra la relation de proportionnalité entre le débit du fluide qui traverse un milieu poreux et la charge hydraulique. Cette équation fondamentale de l’hydraulique permet donc de calculer la perte de charge due à la friction :
|

|
(éq. 3)
|
Avec k la perméabilité [LT-1],  la porosité [sans dimension] et h la charge hydraulique [L].
la porosité [sans dimension] et h la charge hydraulique [L].
33Ce cas correspond à celui présenté sur la Figure 1. Cette configuration correspond au régime naturel d'écoulement de l'aquifère qui fait un angle β constant par rapport à l'horizontal. La charge hydraulique est donc un plan d'équation :
|

|
(éq. 4)
|
34En intégrant l'équation (éq. 4) dans l'équation (éq. 3), donc en appliquant la dérivation, on obtient les vitesses :
|
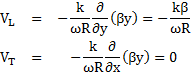
|
(éq. 5)
|
35Ainsi, dans le cas d'un régime naturel, la convection est uniquement longitudinale, seules la diffusion et la dispersion permettent aux particules des mouvements transversaux. Si on intègre l'équation (éq. 5) dans le modèle de transfert (éq. 2), on obtient :
|

|
(éq. 6)
|
36Lorsqu'un forage est mis en place dans un aquifère, plus son débit q est important et plus la charge hydraulique de l'aquifère va être influencée (Figure 5).
Figure 5 : Déformation de la charge hydraulique sous l'influence d'un forage de débit q.

37La détermination de la charge hydraulique h(x,y) en tout point (x,y) de l'aquifère demande de prendre en compte l'ensemble des conditions aux limites de ce système : le forage (appelé également terme source) et la rivière (limite à potentiel imposé, c'est-à-dire que son niveau reste constant, ici à la charge h = 0 m). L'expression de la charge hydraulique h influencée par un forage de débit q dans un milieu infini est bien connue (Marsily (de), 1986) et s'écrit :
|

|
(éq. 7)
|
38Avec r1 la distance entre le point considéré et le forage et R le rayon d'action du forage.
39Le rayon d'action R correspond à la distance au-delà de laquelle le forage n'a plus d'influence sur la charge hydraulique, c'est-à-dire lorsque la charge hydraulique retrouve son régime naturel.
40La prise en compte de la rivière comme limite à potentiel imposé (h = 0 m) nécessite l'utilisation de la méthode des images. En effet, du fait de sa cote constante à h = 0 m, la rivière impose une compensation à la charge hydraulique : lorsqu'on pompe un débit de q m3/s dans l'aquifère, le potentiel imposé de la rivière est équivalent à réinjecter dans l'aquifère un débit de -q m3/s (Figure 6). Ainsi la solution complète de la charge hydraulique en tout point de l'aquifère est la contribution du forage et de la rivière :
|

|
(éq. 8)
|
41Ce qui conduit à (le produit de deux logarithmes est égal au logarithme du produit) :
|

|
(éq. 9)
|
42La Figure 6 permet d'exprimer les rayons r1 et r2 en fonction des coordonnées x et y par le théorème de Pythagore :

43En intégrant la valeur de r1 et r2 dans l'équation (éq. 9), on a successivement :
|

|
(éq. 10)
|
Figure 6 : Principe de la méthode des images pour la prise en compte des conditions aux limites dans le calcul de la charge hydraulique.

44A partir de l'expression de la charge hydraulique (éq. 10), on peut calculer les vitesses associées en utilisant l'équation (éq. 3). Il vient alors successivement :

45Donc dans le cas d'un forage et d'une rivière comme potentiel imposé, les vitesses d'écoulement dans un aquifère sont données par le couple :
|

|
(éq. 11)
|
46Ces vitesses sont calculées à partir de paramètres entrés par l'opérateur (éq. 11), et permettent à une particules de se mouvoir en fonction de sa position (x,y) dans l'aquifère.
47Cet article présente un modèle de transfert de polluants en milieu poreux par une approche multi-agents. Le modèle représente un aquifère connecté hydrauliquement à un cours d'eau. Le modèle simule le transfert d'un polluant et calcule sa concentration en fonction du temps lorsqu'il atteint le cours d’eau. Le modèle est un outil à la fois pédagogique, pour aborder les problématiques de pollutions souterraines auprès des étudiant-e-s, et de recherche afin de donner des ordres de grandeurs et étudier des comportements hydrodynamiques simples.
48Le modèle permet donc d'explorer à la fois l'approche multi-agents proprement dite mais aussi les processus de pollution des eaux souterraines. Pour ce qui concerne l'approche multi-agents, il est par exemple intéressant, pour des paramètres donnés, de changer uniquement le nombre de particules (par exemple 100, puis 1 000, puis 10 000) pour voir comment la courbe de concentration devient plus lisse lorsque ce nombre augmente. En effet, plus on augmente le nombre de particules et plus la discrétisation du nuage de polluant est fine. La courbe de concentration calculée se rapproche donc d'une solution exacte que l'on pourrait obtenir avec la solution de l'équation différentielle (éq. 12).
49Pour explorer l'influence du forage sur la dynamique du polluant, on peut par exemple, pour des paramètres donnés, changer uniquement la valeur du débit du forage (par exemple 0, puis 0.01 m3/s) et voir comment la charge hydraulique est modifiée et donc comment la trajectoire des particules est influencée. On peut également garder la trace moyenne de ces trajectoires, en positionnant le bouton “Trace” sur “On”, afin de voir le décalage spatiale de cette trajectoire lorsque la valeur du forage est augmentée.
50Pour explorer l'influence de la taille de la source pour des paramètres donnés, on peut changer la taille de la source (par exemple 0 puis 50 m) et voir comment la forme initiale de cette source modifie l’évolution de la concentration du polluant dans la rivière. Plus la source est grande et plus la dispersion de la concentration dans la rivière est importante. Si on positionne le bouton “Trace” sur “On”, on voit en revanche que la trajectoire moyenne n'est pas modifiée.
51Les possibilités d'exploration sont importantes et peuvent encore être complexifiées en programmant NetLogo : plusieurs sources de polluants, plusieurs forages, ou encore une charge hydraulique qui fluctuerait dans le temps en fonction des précipitations. La rivière pourrait également être remplacée par une étendue d'eau salée (mer ou océan) afin d'explorer les problématiques d'intrusion du biseau salé. La comparaison avec une étude de cas réel pourrait également être envisagée en affectant au Monde de NetLogo les bonnes dimensions (Settings) et en introduisant sur graphique la concentration réelle du polluant. Enfin, il est aisé d'adapter les équations du transfert en 3D, mais là NetLogo n'est plus du tout adapté : le temps de calcul est bien trop important. Dans ce cas il est préférable d'envisager une programmation à compiler de type Fortran, C ou encore C++.
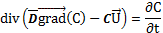




 ). Les variables locales ou microscopiques sont (xi,yi) et les variables globales ou macroscopiques sont (X, Y).
). Les variables locales ou microscopiques sont (xi,yi) et les variables globales ou macroscopiques sont (X, Y).



 sont donc nulles) :
sont donc nulles) :
 la vitesse moyenne, Δt le pas de temps,
la vitesse moyenne, Δt le pas de temps,  et
et  les coefficients de dispersion longitudinale et transversale respectivement,
les coefficients de dispersion longitudinale et transversale respectivement, 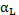 et
et  les dispersivités longitudinale et transversale respectivement, Z1 et Z2 sont des nombres aléatoires de distribution uniforme entre -1 et 1.
les dispersivités longitudinale et transversale respectivement, Z1 et Z2 sont des nombres aléatoires de distribution uniforme entre -1 et 1.
 la vitesse moyenne de pore [LT-1], D le tenseur de dispersion [L2T-1] et R le coefficient de retard.
la vitesse moyenne de pore [LT-1], D le tenseur de dispersion [L2T-1] et R le coefficient de retard.
 la porosité [sans dimension] et h la charge hydraulique [L].
la porosité [sans dimension] et h la charge hydraulique [L].
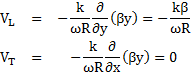










 un vecteur perpendiculaire sortant à la surface enveloppe de ce volume), alors l’expression mathématique de ce flux convectif s’écrit :
un vecteur perpendiculaire sortant à la surface enveloppe de ce volume), alors l’expression mathématique de ce flux convectif s’écrit :
 la vitesse moyenne de pore [LT-1] dans le milieu poreux.
la vitesse moyenne de pore [LT-1] dans le milieu poreux.


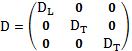



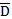 est le tenseur de diffusion-dispersion [LT-2], symétrique et du second ordre qui associe donc le coefficient de diffusion moléculaire et le tenseur de dispersion.
est le tenseur de diffusion-dispersion [LT-2], symétrique et du second ordre qui associe donc le coefficient de diffusion moléculaire et le tenseur de dispersion.


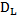 est le coefficient de dispersion [LT-2] longitudinal et Vm la vitesse moyenne de pore [LT-1]. Pour une injection instantanée d'une masse M de polluant (ce qui est le cas dans le modèle présenté ici), la solution de l'équation de transfert en monodimensionnel est :
est le coefficient de dispersion [LT-2] longitudinal et Vm la vitesse moyenne de pore [LT-1]. Pour une injection instantanée d'une masse M de polluant (ce qui est le cas dans le modèle présenté ici), la solution de l'équation de transfert en monodimensionnel est :

 est la dispersivité du milieu considéré et Dm le coefficient de diffusion moléculaire en milieu poreux.
est la dispersivité du milieu considéré et Dm le coefficient de diffusion moléculaire en milieu poreux.





