1Depuis le milieu des années 1990, la simulation informatique et les méthodes individu-centrées connaissent de nombreux développements dans les sciences sociales. Ces méthodes offrent la possibilité de modéliser directement les comportements et les interactions au niveau des entités élémentaires d’un système afin de simuler la dynamique d’un phénomène à un niveau supérieur. Il s’agit ainsi d’expliquer comment des dynamiques et des régularités présentes à un niveau global d’observation peuvent émerger des interactions qui se produisent à un niveau jusqu’ici mis de côté par les méthodes classiques de modélisation, le niveau local. Mais il s’agit également d’explorer les effets de ces phénomènes émergents sur l’évolution des comportements individuels : il ne suffit plus d’observer de manière distincte l’univers collectif et l’univers individuel, il peut être pertinent d’étudier les relations entre les deux. Ainsi, comme le souligne J. Holland (1998) : « What people believe affect what happens to the economy and what happens to the economy affects what people believe ». Cet argument trouve son écho dans les sciences de la complexité au rang desquelles se situent les théories de la vie artificielle et de l’intelligence artificielle distribuée.
2L’intérêt de cette approche est discuté ici au regard des limites rencontrées par l’utilisation des modèles macro traditionnellement employés pour modéliser les processus de diffusion. L’équation logistique est ainsi présentée comme un exemple de cette catégorie de modèle. La modélisation individu-centrée et les systèmes multi-agents sont ensuite exposés comme une alternative à ces approches globales. Cet article se termine par un exemple d’application, la modélisation et la simulation de la diffusion d’une innovation agricole.
3Il est classique en analyse spatiale de décrire et de modéliser les phénomènes observés à un certain niveau en posant des hypothèses et des équations qui sont opératoires à ce niveau d’observation. Par exemple la diffusion d’une activité économique au niveau d’un système urbain sera modélisée en posant des hypothèses propres à ce niveau d’observation : l’intensité et le déplacement de la nouveauté sont fonctions de la taille des villes, qui sont ici les entités élémentaires du système, et de la distance qui les sépare. Dans ce contexte, on postule que la structure globale du système urbain s’impose aux entités élémentaires qui le composent, c’est-à-dire les villes, et aux dynamiques qui s’y déploient. Si cette approche macro permet de décrire correctement certaines diffusions, elle n’offre cependant qu’une explication partielle des véritables mécanismes qui en sont responsables. Au mieux cette explication vient après la formalisation mathématique ou statistique, par la mise en évidence de facteurs complémentaires à ceux privilégiés lors de la modélisation. Cette phase contribue alors à dépasser les limites des modélisations traditionnelles, qui obligent à poser des hypothèses restrictives par rapport aux hypothèses théoriques que l’on a du phénomène observé. Le modèle logistique constitue à ce titre un bon exemple.
4La diffusion par contagion exprime l’idée que ce qui apparaît en un lieu est en partie fonction de ce qui s’est déjà produit dans des lieux proches, idée que l’on retrouve dans le concept statistique d’autocorrélation spatiale. De manière similaire, la courbe en S ou courbe logistique (Hägerstrand, 1952) met en évidence le poids des événements passés sur les événements à venir, mesuré par l’autocorrélation temporelle. Lorsque le phénomène étudié se caractérise à la fois par une autocorrélation temporelle et spatiale, une forme spatio-temporelle assimilable à des vagues de diffusion peut être observée (Morrill, 1968).
5Revenons cependant par souci de simplification à la seule forme temporelle de la diffusion formalisable par la fonction logistique. Ce modèle élémentaire de contagion – ou modèle de pure imitation ou encore d’influence interne (Mahajan et Peterson, 1985) – rend compte du taux d’adoption au temps tn comme une fonction du nombre d’individus ayant déjà adopté en tn-1. Si A(t) représente le nombre d’individus ayant adopté l’innovation au temps t et P la taille de la population ou le nombre d’individus susceptibles d’adopter l’innovation en début de période (t0), on peut écrire l’équation différentielle suivante :
6Dans ce modèle, r est une constante qui représente le taux de propagation sur l’ensemble de la période et [P - A (t)] le nombre d’individus n’ayant pas encore adopté l’innovation à l’instant t. En supposant qu’à l’instant t = 0, A vaut 1, on obtient par intégration :
- 1 Lorsque A est infiniment petit par rapport à P, alors A(t) ≈ eP.r.t
7Le nombre d’individus atteints en fonction du temps suit donc une loi exponentielle1 et cette fonction peut être assimilée à une loi de croissance.
8Dans la plupart des cas, l’information dont on dispose se présente sous la forme de données agrégées et ex-post, c’est-à-dire une fois la diffusion terminée. Le modèle logistique est construit à partir de ce type d’information, où la donnée de base représente des agrégats d’adoptants dans le temps. La modélisation consiste alors le plus souvent à adapter une fonction mathématique à ces informations, en ajustant les différents paramètres de l’équation. Ce point de vue agrégé, qui consiste à s’intéresser au comportement de l’ensemble, implique de faire un certain nombre d’hypothèses sur le comportement des individus qui composent cet agrégat.
9Le nombre d’individus est suffisamment important pour exclure toute influence individuelle sur le devenir de la diffusion, c’est l’hypothèse d’atomicité. Cette hypothèse est renforcée par l’hypothèse d’homogénéité du comportement, les individus composant la population étant caractérisés par une identité parfaite et substituable. Si ces hypothèses permettent de définir le paramètre d’évolution de la propagation dans le temps et donc de comparer différentes diffusions, elles deviennent restrictives lorsqu’on tente d’appréhender la diffusion d’un point de vue explicatif, car, dans ce cas, comment expliquer les différences d’adoption dans le temps ? Si les individus ont tous le même comportement, qu’est ce qui différencie les individus qui « adoptent » précocement des individus qui « adoptent » tardivement ?
10L’information dans ce type de modèle circule librement et elle est universelle, tous les individus disposent de la même information sur le nombre d’adoptants effectifs et potentiels. L’hypothèse implicite est que tous les agents se connaissent, s’observent, et que les contacts s’établissent de manière aléatoire parmi les membres du système analysé (Bailey, 1957). Si cette hypothèse est commode pour ajuster une fonction à des données agrégées, elle pose également un problème heuristique, que l’on soit sociologue ou géographe. On peut en effet considérer que c’est l’hétérogénéité spatiale et/ou sociale ainsi que l’existence de mécanismes différenciés d’accès à l’information qui expliquent en partie que la diffusion soit un processus qui s’inscrit dans le temps et qui n’atteint pas tous les lieux ou tous les individus composant un groupe.
11La fonction de décision de l’individu est discrète et non dynamique. L’individu est soit adoptant (1) soit non adoptant (0), sa décision ne dépend pas d’un processus d’apprentissage de l’innovation et il ne peut remettre en cause son choix une fois sa décision prise. La non prise en compte d’un modèle dynamique d’évolution de l’état des individus face à la question de l’adoption exclut donc d’importants facteurs qui rendent compte de la réalité, mais est toutefois nécessaire si l’on veut respecter les deux premières hypothèses. Cette formulation montre bien que l’on ne modélise que les succès ex-post, ce qui laisse peu de place à une modélisation dans un but prédictif. Le rejet de l’innovation, l’échec de la diffusion, l’existence de seuils à partir desquels un retour en arrière est peu probable devraient faire partie des questions relatives à une étude de diffusion.
12Une fois introduite dans un système, cette catégorie de modèle postule implicitement que l’innovation n’évolue pas. Les caractéristiques de l’objet introduit sont strictement identiques entre le lieu et le temps de son apparition dans le système et le moment où il s’est entièrement propagé. Si cette hypothèse ne pose a priori pas de difficulté lorsqu’elle concerne la propagation d’un incendie, elle devient plus contraignante lorsqu’elle s’applique à une innovation technologique. Entre le moment de son apparition et le stade final de diffusion, les caractéristiques de l’objet nouveau peuvent en effet être totalement modifiées : d’un point de vue technique, dans son prix, dans sa complexité d’utilisation, dans les types d’utilisation que les adoptants en font etc. Cette dynamique de l’innovation a une incidence potentiellement très importante sur le taux d’adoption, sur la temporalité de l’adoption et sur les lieux de l’adoption. En tant qu’innovation dans le domaine productif, le travail intérimaire par exemple tend à évoluer du secteur secondaire vers le secteur tertiaire, ce qui ne sera pas sans conséquence sur les zones spécialisées dans les secteurs des services ou du tourisme qui jusqu’à présent ont été « épargnées » par ce type d’activité (Daudé, 2002a).
13Malgré leurs limites, toutes ces hypothèses sont nécessaires et fournissent un cadre rigide qui permet de décrire certaines régularités d’ordre global et offrent des solutions analytiques simples. Ces modèles tendent finalement à simplifier des phénomènes éminemment complexes, en surestimant le poids du processus modélisé et en sous-estimant le rôle des autres processus à l’œuvre lors de la diffusion. Ultimo, même une modification de l’hypothèse d’homogénéité du comportement des individus laisserait apparaître une courbe logistique du simple fait de la constance de la population et de la non prise en compte de changements d’attitude face à l’adoption de l’innovation.
14Comme le souligne P. Gould (1992), la méconnaissance des véritables processus à l’œuvre lors d’une diffusion a entraîné le développement et le raffinement de modèles ayant une faible portée prédictive et explicative. Ces modèles ne sont alors pas aptes à produire autre chose que ce que l’on attend, car les règles ou les mécanismes qui y sont intégrés ne laissent que peu de place au changement. Or la diffusion est un phénomène dynamique, soumis à des perturbations et des changements permanents qui peuvent malgré tout produire des régularités. L’objectif est grand de proposer des modèles aptes à prendre en compte cette complexité tout en proposant, sous certaines conditions, des solutions proches de nos observations. Les approches individu-centrées offrent alors de nouvelles perspectives dans l’exploration de tels processus.
15La diffusion est liée à un ensemble d’actions pouvant conduire à diverses trajectoires, du succès à l’échec de diffusion de l’innovation. L’objectif est alors de construire des modèles capables de générer cette diversité des futurs possibles, rompant ainsi avec une tradition de modélisation des seuls succès de diffusion. Dans ce contexte, on pose l’hypothèse qu’en se situant au niveau des entités élémentaires, c’est-à-dire au niveau des unités décisionnelles de base, il est possible de proposer ce type de modèle. On postule ainsi que la répétition de processus plus ou moins élaborés au niveau individuel a une incidence sur le devenir de la diffusion à un niveau global, à la fois dans les taux de propagation, leurs distributions spatiales et la vitesse de diffusion de l’innovation. Il reste alors à décrire les éléments qui paraissent jouer un rôle essentiel au niveau local pour rendre compte de possibles observations à un niveau agrégé. Il s’agira ainsi de dépasser les limites mentionnées quant aux hypothèses des modèles agrégés (voir § 8), principalement sur l’homogénéité des comportements individuels, sur la circulation globale de l’information et sur l’aspect statique des caractéristiques de l’innovation.
16La réalisation d’une diffusion exige la présence d’un ou de plusieurs émetteurs et d’un potentiel d’adoptants. Outre une distinction selon cette catégorisation, il existe de nombreux facteurs de différenciation entre individus appartenant à un groupe, diversité qui a des conséquences sur l’évolution du phénomène. La diversité des aptitudes innovantes des individus peut par exemple expliquer qu’une innovation se diffuse sur une certaine durée. Ainsi selon les théories sociales d’E. Rogers (1995), les individus peuvent être schématiquement classés en cinq groupes selon leurs aptitudes à adopter plus ou moins rapidement l’innovation : les innovants (1), les adoptants précoces (2), la majorité précoce (3), la majorité tardive (4) et les retardataires (5). A chacune de ces catégories correspond une fonction de décision dynamique qui amène l’individu à faire son choix plus ou moins rapidement. Celle-ci peut être liée à ses objectifs, à ses contraintes financières, à son insertion dans des réseaux relationnels plus ou moins complexes etc. On peut alors rapprocher ces différentes catégories de la courbe du taux d’adoption et donner ainsi une explication plus réaliste au temps de la diffusion (figure 1). Il y a ainsi une étroite articulation entre les approches macro et les approches individu-centrées : s’il est nécessaire de rendre plus réalistes les hypothèses sur les comportements des individus, cette diversité peut produire malgré tout des formes régulières (temporelles et/ou spatiales) à un niveau supérieur, régularités formalisables à l’aide de lois ou de modèles relativement simples, telle que la fonction logistique.

Figure 1 - Une typologie des aptitudes individuelles face à l’adoption
17Outre les caractéristiques individuelles, l’information relative à une innovation a une incidence sur sa diffusion. Or les vecteurs de circulation de l’information sont nombreux, que ce soit par les médias ou par contacts interpersonnels. Selon l’innovation concernée, le type de système dans lequel elle s’insère et les profils individuels, le poids de cette mise en contact avec l’innovation peut varier, il s’agit alors de repérer dans le système étudié les principaux canaux de circulation de l’information. Dans le cadre d’une approche individu-centrée, on considère que l’information circule principalement entre les individus. Ceci implique que les individus ne disposent que d’une information partielle, à la fois sur les caractéristiques de l’innovation mais également sur l’attitude des autres agents face à l’adoption ou au rejet. Cette connaissance se construit peu à peu, en fonction des interactions entre agents proches, d’un point de vue spatial mais pas seulement. Les interactions se traduisent alors par des échanges d’information et par une évolution des décisions individuelles.
18Enfin la diffusion se réalise dans la durée, ce qui implique que les choix individuels sont le résultat de processus décisionnels dynamiques et que l’innovation elle-même est capable d’évolution. Ceci pose la question de l’impact des caractéristiques de l’innovation et de leurs évolutions sur la dynamique de diffusion. Les caractéristiques de l’innovation ont une influence sur les décisions individuelles car celle-ci n’offre pas les mêmes attraits pour tous les individus : le prix d’une innovation ne représente pas la même contrainte pour tous les individus. Mais cette innovation peut évoluer dans le temps, en fonction des expériences, des pratiques ou des normes, et modifier en retour les comportements individuels. Ce type de mécanisme se produit par exemple lorsque l’innovation est un bien marchand et que sa diffusion dans une proportion de plus en plus importante de la population agit sur son prix, et donc sur l’évolution des choix individuels d’adoption. Il s’agit alors de prendre en compte le fait que les processus individuels qui produisent des phénomènes à un niveau meso ou macro évoluent dans le temps, en fonction de certains seuils atteints à un niveau supérieur. Ces phénomènes de rétroaction du niveau macro sur les comportements individuels sont des émergences de second ordre (Gilbert, 1995).
- 2 La définition du niveau élémentaire est fondamentalement liée à la problématique et au problème à r (...)
19Il est donc possible de poser à la fois des hypothèses sur l’hétérogénéité des comportements individuels, sur le poids des interactions entre ces entités élémentaires2 et sur l’importance des caractéristiques de l’innovation et leurs évolutions dans la diffusion. Ces différentes hypothèses modélisées au niveau individuel sont susceptibles de faire émerger certaines régularités à un niveau global (figure 2).
Figure 2 - Interactions locales et régularités globales
20Selon ce point de vue, la fonction logistique ou une diffusion selon la hiérarchie des lieux sont produits par le jeu des interactions à des niveaux inférieurs et peuvent être considérés comme des phénomènes émergents persistants. L’émergence est donc un concept ascendant, des règles propres à un niveau micro produisent des règles propres à un niveau macro (Wilensky et Resnick, 1998). Ces propositions permettent alors de situer les phénomènes de diffusion selon les perspectives des théories de l’auto-organisation.
21La théorie de l’auto-organisation a initialement été développée par les physiciens et les chimistes pour décrire comment des processus microscopiques pouvaient générer des structures macroscopiques. Au sens des physiciens, l’auto-organisation renvoie à la capacité que possède une population d’entités simples à se structurer spatio-temporellement et ce en échangeant de l’énergie avec son environnement. De tels systèmes se caractérisent par une ouverture de la population sur l’environnement avec lequel elle interagit : les interactions entre les éléments sont affectées par les paramètres de l’environnement du système, et ces interactions peuvent modifier en retour cet environnement. Les règles d’interactions entre les entités élémentaires du système sont exécutées à partir d’informations strictement locales, sans référence ou intervention du modèle global ni même de l’extérieur, du moins pas principalement. Ces processus engendrent et entretiennent la propriété du système, propriété qui est émergente car elle n’est pas imposée au système par un quelconque « chorégraphe invisible » (Kauffman, 1995).
22Les phénomènes auto-organisés présentent la particularité de ne pas être pilotés ou contrôlés par des éléments qui agissent à des niveaux supérieurs mais sont le résultat des seules interactions entre les entités élémentaires du système, celles-ci n’ayant aucun objectif d’ordre global et ne disposant que d’une vision limitée, locale, de leur environnement. Ainsi certaines propriétés d’un système sont émergentes parce qu’elles apparaissent à un niveau global d’observation et qu’elles ne sont pas déductibles de la simple observation des éléments qui opèrent à un niveau local : l’observation d’un individu ou de l’ensemble des individus d’une population ne permet pas de prédire si une diffusion va se réaliser ou pas.
23La nature décentralisée des phénomènes auto-organisés est en partie vérifiée pour les phénomènes de diffusion, car les exemples de diffusion totalement planifiée se conformant avec précision aux plans originels sont peu nombreux. Cependant, à l’instar des travaux de L. Brown (1981) et en conservant l’idée que les phénomènes de diffusion sont des phénomènes émergents, en ce sens qu’ils ne se contrôlent pas ou seulement partiellement, on peut parler d’un impératif téléologique pour ceux qui tentent de la contrôler. S’il n’y a pas contrôle à proprement parler, l’intentionnalité est bien présente : des acteurs se donnent les moyens de créer les opportunités pour que la diffusion se réalise, et donc de créer les conditions de l’émergence en « ouvrant » des trajectoires possibles. Si la diffusion ne se pilote pas car le niveau d’adoption dépend du comportement des individus, les conditions peuvent ainsi être créées pour que la diffusion se réalise selon une certaine tendance. Dans ce contexte, on peut parfois prédire qu’il y aura émergence sans pouvoir estimer le niveau d’adoption, les lieux et le temps de l’adoption.
24Outre la nature décentralisée des phénomènes de propagation, les mécanismes qui mènent à leur émergence sont également communs aux phénomènes auto-organisés. Les phénomènes d’amplification, par le biais des rétroactions positives, sont à l’origine de nombreuses propagations de produits de consommation de masse. Pour ces produits, l’accroissement du nombre d’utilisateurs fonctionne selon un effet « boule de neige », à l’image du fax ou du téléphone : l’utilité de la nouveauté est faible lorsque l’innovation apparaît, car il y peu d’utilisateurs, mais celle-ci augmente rapidement, au fur et à mesure que le volume d’utilisateurs s’accroît. Les effets stabilisateurs, avec les rétroactions négatives, sont également importants pour les phénomènes qui se propagent dans un système. La stabilisation peut prendre la forme de saturation, car le nombre limité d’adoptants potentiels amène l’innovation à son stade final d’adoption, tel qu’on le formalise avec la fonction logistique. La stabilisation peut également se réaliser par le biais de l’épuisement des ressources nécessaires à la diffusion, comme c’est le cas pour la propagation des incendies ou pour l’exploitation de ressources naturelles dans les fronts pionniers. Enfin la stabilisation peut être le résultat de la concurrence entre diverses innovations, car une innovation est très rarement exclusive sur un marché, elle est souvent en compétition avec d’autres innovations avec lesquelles elle partage le même segment de marché.
25Les phénomènes qui se diffusent dans un système peuvent enfin être analysés selon le point de vue de l’auto-organisation dans la mesure où, dans bien des cas, les agents se réapproprient l’innovation, la modifient, en font de nouveaux usages. De nombreuses innovations doivent leur succès à cette réappropriation de l’objet par les individus, indépendamment des objectifs initiaux des concepteurs de l’innovation : le téléphone, le Minitel, Internet en sont des exemples. Cette réappropriation de l’objet par les individus accentue l’imprévisibilité de la diffusion à un niveau global, mais ne doit cependant pas décourager toute tentative d’étude de ces phénomènes. L’approche par la théorie de l’auto-organisation peut nous éclairer sur les formes possibles de l’évolution d’une diffusion, nous apporter une vision prospective des différentes trajectoires possibles du phénomène.
26Mais l’auto-organisation n’est pas un mécanisme universel car d’autres mécanismes peuvent être à l’origine de modèles globaux d’un système, même si les individus qui le composent ne sont pas « conscients » de ces mécanismes. Cette remarque est d’autant plus pertinente en géographie que bien des phénomènes s’inscrivent dans un espace structuré qui va contraindre le comportement des individus : un individu n’est pas forcément conscient que l’objet qu’il adopte à un moment donné et en un lieu donné ne se réalise que parce que ce lieu est intégré à un système global, celui des villes par exemple, et que celui-ci conditionne largement la circulation des hommes et des informations et donc la disponibilité de l’innovation. Ces pré-modèles, comme les appellent les entomologistes (Bonabeau et al., 1997), ont un poids non négligeable dans nombre de phénomènes car ils peuvent orienter les formes produites ou dans notre cas, les voies prises par la propagation. Dans ce cas, le phénomène que l’on observe à un niveau global est tributaire en partie de l’environnement dans lequel les individus vivent et interagissent, celui-ci devant alors être pris en compte dans l’explication du phénomène. Ainsi, même si elles ne peuvent entièrement appréhender les phénomènes, les théories de l’auto-organisation proposent un environnement pour comprendre comment les systèmes fonctionnent de manière dynamique et interactive, et offrent des techniques pour simuler de tels phénomènes.
27Les sciences de la complexité proposent un retour sur les comportements individuels, elles postulent que les régularités observées à un niveau macro peuvent être rendues cohérentes en posant des hypothèses sur les comportements des entités élémentaires qui composent le système étudié. La principale difficulté consistait jusqu’alors, compte tenu des méthodes à la disposition du chercheur, à observer dans le temps et dans l’espace le « comportement » d’hypothèses posées à ce niveau. La simulation informatique rend cet exercice possible, elle offre la possibilité de créer un monde artificiel à partir de théories, de lois et d’hypothèses et permet d’observer le comportement de cet artefact sur quelques aspects lorsque certains paramètres du modèle sont soumis à variation. Parmi les méthodes aujourd’hui disponibles, les systèmes multi-agents (SMA) apportent de nombreuses possibilités au modélisateur.
28Un SMA est un programme informatique composé d’agents, des entités informatiques autonomes capable d’agir sur elles-mêmes et sur leur environnement. Dans un univers multi-agents, l’agent peut communiquer avec d’autres agents et se déplacer, mais pas nécessairement. Son comportement est alors la conséquence de ses observations, de ses compétences et des interactions avec les autres agents (Ferber, 1995). Le temps est directement intégré sous la forme d’une horloge qui rythme les séquences d’actions des agents. Les SMA sont donc des modèles essentiellement d’interactions, la dynamique du phénomène étudié étant le produit de ces interactions.
29Selon une problématique de diffusion appréhendée au travers d’une modélisation multi-agents, il est possible de poser l’hypothèse que ce sont l’hétérogénéité des situations spatiales et sociales et la diversité des comportements individuels qui sont les principaux moteurs des dynamiques de propagation. Dans ce contexte, la compétence d’un agent relève en partie de son aptitude à innover, ses connaissances relèvent en partie de ses observations et tout ceci est lié aux nombreuses interactions et communications qu’il entretient avec les autres agents. Cette diversité des situations doit permettre de décrire et expliquer des phénomènes que l’on observe généralement à un niveau agrégé. Les SMA offrent également la possibilité de réintroduire de la réciprocité entre une approche micro et une approche macro, car si les individus sont à l’origine des structures sociales et spatiales, celles-ci peuvent contraindre en retour le comportement de ces individus.
30Un modèle multi-agents a été développé pour simuler la diffusion d’une innovation agricole (Daudé, 2002b). Outre l’aspect heuristique de la méthode, celle-ci permet de tester des hypothèses et favorise l’intégration dans une seule simulation de différents aspects présents dans la littérature qui, pris séparément, ne permettent pas d’expliquer la complexité d’un tel phénomène. Cette méthode laisse alors entrevoir une possibilité d’exploration prédictive des phénomènes qui s’exercent dans l’espace géographique. Sont présentés ici les principaux mécanismes modélisés ainsi que les résultats des dernières simulations réalisées.
31L’innovation concernée dans cette étude est une subvention à la pratique du pâturage en Suède. Cette innovation et sa diffusion ont été étudiées par T. Hägerstrand et ont donné lieu à l’une des premières simulations en sciences sociales (Hägerstrand, 1952). Dans le modèle développé par cet auteur, la diffusion est appréhendée comme un processus spatial et sa modélisation montre le poids de la spatialité – mesuré ici en terme de contiguïté – dans la propagation de l’innovation. La diffusion est ainsi un processus qui met en contact des émetteurs et des récepteurs et il suffit de connaître les principaux canaux de circulation de l’information pour être en mesure de déterminer le déplacement de l’innovation dans l’espace.
- 3 On pourra se reporter à T. Hägerstrand (1965) ou à T. Saint-Julien (1985) pour une description déta (...)
- 4 T. Hägerstrand réalise des simulations pour atteindre approximativement le nombre d’adoptants recen (...)
32Partant de l’hypothèse que les contacts entre individus sont le principal vecteur d’information et de diffusion, Torsten Hägerstrand construit une grille d’interaction spatiale, le champ moyen d’information, et modélise le processus de communication et d’adoption des individus. L’acceptation de l’innovation par un individu se fait immédiatement après qu’il ait pris connaissance de son existence, i.e. lorsqu’un individu l’ayant déjà adopté lui transmet un message sur son existence3. La figure 3 montre la diffusion telle qu’on a pu l’observer sur le terrain, les résultats d’une simulation à partir du modèle de T. Hägerstrand (1965) ainsi que les principaux écarts pour l’année 19444.
Figure 3 - Diffusion observée et simulée des subventions

33Un système multi-agents5 a été développé afin d’explorer les potentialités de cette méthode dans un questionnement géographique, tant dans la validité des hypothèses posées que dans la cohérence des résultats simulés (Daudé, 2002b). Le modèle prend en compte la diversité individuelle telle qu’elle a été présentée précédemment (voir § 16), l’existence de réseaux relationnels privilégiés entre les agents6 et les caractéristiques de l’innovation ainsi que leurs évolutions (figure 4). Les agents se distinguent par une fonction de décision dynamique qui les conduit à accepter ou à rejeter l’innovation. Cette fonction est soumise à une certaine probabilité (x) qui évolue en fonction des catégories de messages (m) qu’ils reçoivent et des caractéristiques de l’innovation, décrite au départ sous la forme d’un indice. Cet indice est étalonné à l’initialisation afin que les simulations produisent au final un taux d’adoption global sensiblement équivalent à celui observé en 1944. Le temps nécessaire à chacun des agents pour effectuer un choix est fonction de son aptitude innovante (S) telle qu’elle a été définie précédemment. Ils ont alors la possibilité, selon leur état, d’envoyer des messages positifs (négatifs) aux agents qui font partie de leurs réseaux de relation et ceci favorise l’acceptation (le rejet) de l’innovation par les agents qui les reçoivent. Ces informations tendent en effet à diminuer ou à augmenter la probabilité d’adoption de l’individu selon des pondérations différenciées affectées aux messages. On considère que les informations négatives peuvent avoir une incidence (r1) autre sur la probabilité individuelle d’adoption que les messages positifs (r2). Les agents qui n’ont pas encore arrêté leur choix concernant l’innovation ont également la possibilité d’observer leur environnement afin d’évaluer leurs actions futures. Ainsi la probabilité qu’un agent adopte (rejette) les subventions augmente s’il est en mesure d’observer dans son environnement proche un nombre important d’agents qui ont adopté (rejeté) cette innovation.
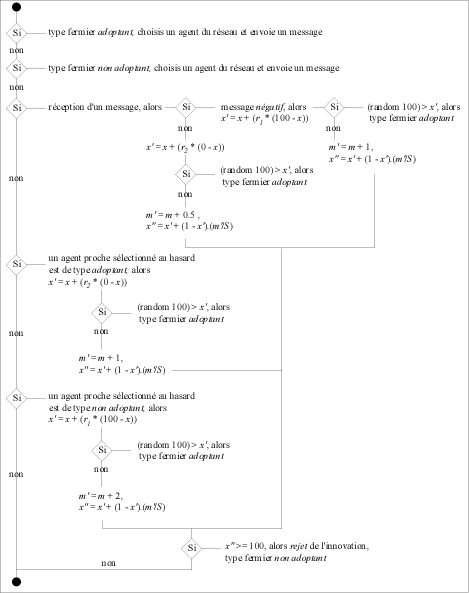
Figure 4 - Possibilités comportementales de l’agent fermier au cours d’une itération
34Ces différents mécanismes qui se jouent principalement à une échelle locale produisent lors des simulations une autocorrélation spatiale des résidus, en accentuant les tendances locales des taux de pénétration. Ces résultats nous ont alors amené à reformuler les hypothèses sur la dynamique de diffusion de cette innovation. Ils ont notamment conduit à introduire un mécanisme agissant à un niveau d’organisation supérieur à celui de l’individu.
35A leur lancement, les subventions ont un fort pouvoir attractif sur les fermiers car les informations véhiculées par les médias mettent en avant de nombreux avantages, les probabilités individuelles d’adopter sont alors élevées. Le nombre de fermiers qui adoptent cette pratique agricole croît ainsi de manière exponentielle durant les premières années. Malgré les nombreux avantages supposés, quelques fermiers rejettent cependant les subventions en entraînant dans leurs sillages, localement, d’autres fermiers. Ce phénomène n’a cependant pas de répercussions d’ordre global immédiat. C’est en fait la pratique du pâturage subventionné qui va avoir le plus d’effets sur la dynamique à venir de sa diffusion : les résultats associés à la pratique des pâturages par les fermiers et l’intérêt des subventions s’avèrent peu à peu moins bénéfiques qu’initialement prévu. Il est probable que cette information a rapidement circulé parmi les fermiers, mettant ainsi en évidence l’existence d’une émergence de second ordre. Une boucle de rétroaction négative se met alors en place, lorsque les informations collectives confirment la tendance enclenchée à un niveau local. La figure 5 illustre ces diverses dynamiques, elle montre le déplacement de la diffusion et les taux d’adoption locaux pour une simulation, ainsi que les écarts entre une moyenne de 50 simulations et l’état de la diffusion observée en 1944.

Figure 5 - Simulations et écarts à partir d’une modélisation individu, espace et innovation
- 7 Ce résultat tombe à moins de 30% à partir du modèle strictement spatial de T. Hägerstrand (1965).
36Le modèle permet ainsi de représenter correctement plus de 58% des taux de propagation observés en 19447, ce qui est un résultat plutôt satisfaisant compte tenu de la simplicité du comportement des agents fermiers. Ces résultats confirment ainsi en partie les hypothèses posées sur les éléments essentiels responsables de la diffusion et des taux de propagation des subventions dans la zone. Certains écarts subsistent cependant, notamment dans la partie occidentale de la zone : certains fermiers ont rejeté les subventions après les avoir acceptées, ce qui n’est pas pris en compte dans le modèle. De même les foyers initialement touchés par les subventions en 1929 et situés dans la partie nord-est de la zone n’ont pas eu un rôle aussi important dans la transmission des informations que les foyers de la partie ouest. Les raisons de ce déséquilibre n’ont pas été éclaircies, seules des hypothèses peuvent être avancées : un tissu social moins serré, une propension à innover moins importante pour les fermiers de l’est etc.
37La diffusion d’une innovation est un résultat que l’on peut observer et décrire à un niveau macro, c’est également un ensemble de processus que l’on peut modéliser à un niveau micro. Selon ce point de vue, le modèle doit être en mesure de générer des résultats que l’on observe à un niveau global à partir de certaines combinaisons paramétriques, mais il peut également produire d’autres résultats lorsque certains paramètres sont soumis à variation. Ceci implique de considérer les phénomènes observés comme un résultat parmi un ensemble de résultats envisageables, ouvrant ainsi la porte à l’exploration de futurs possibles.
38Un raisonnement strictement spatial ne permet pas d’expliquer l’arrêt (ou l’accélération) de certaines diffusions ou des différences de taux d’adoption entre lieux équivalents. Au-delà des interactions spatiales, de la position relative et de la localisation des hommes et des activités, l’évolution de la diffusion dépend notamment du comportement des individus et des caractéristiques des innovations qu’ils sont susceptibles d’adopter. L’enjeu est alors de rendre plus réalistes les études sur la diffusion spatiale des innovations, en intégrant les processus qui agissent de manière prépondérante sur la diffusion. Or chaque innovation possède des caractéristiques qui lui sont propres, s’insère dans des systèmes économiques ou sociaux différenciés, est susceptible d’être contrôlée ou non par un organisme responsable de sa diffusion etc., ce qui tend à rendre les recherches dans ce domaine particulièrement complexes. Mais ce constat ne signifie pas que des règles générales ne puissent être découvertes dans chacun de ces cas, l’exemple de la diffusion des subventions aux pâturages en est un exemple. A partir d’un raisonnement spatial qui privilégie le poids de la distance dans les canaux de propagation de l’information, d’un raisonnement social qui met en avant le rôle des réseaux relationnels, des contacts interpersonnels et de l’hétérogénéité de la population, et d’un raisonnement sur l’innovation elle-même, susceptible d’évoluer dans ses caractéristiques, ce sont alors près de 60% des unités spatiales de la zone d’étude qui sont bien représentées par le modèle.












